中２の数学の授業で、「モンティ・ホール問題」という、「直感的な解答」と「実際の解答」が一致し難い確率の問題を紙コップとサイコロを使って実験して考えてみました。

実験器具
紙コップ×3
サイコロ(あたりの代わり)×1

役割
司会者／プレイヤー／記録係

実験方法
① 3つのコップ(A,B,C)に、司会者がランダムでサイコロを入れます。
② プレイヤーはコップを 3つのうち 1 つ選びます。
③ 司会者は残りのコップ2つのうち、ハズレのコップを開けます。
④ プレイヤーは未開のコップ2つのうち、最初に選んだコップから残りのコップに変更するか、変更しないか選択できます。

ここで、最初に選んだコップから変更した方が的中率が上がるのか、変更しない方が的中率が上がるか、どちらを選択しても的中率が変わらないかを予想しました。

「あたり,ハズレ,ハズレから 1 つ選んだ後にハズレの 1 つが消えるため、変えても変えなくてもあたり,ハズレの 2 つから 1 つ選ぶので確率は 1/2なのでは…？」
「選択を変えない場合、あたり、ハズレ、ハズレの 3 つから 1 つ選ぶので確率は 1/3 になるよね…？」
様々な意見が出たところで、グループを作り、１～３班は「最初から変更する」班と「最初から変更しない」班に分かれて、繰り返し実験し、それぞれの的中率を求めました。
 

その結果、「変更した」場合の的中率は約66％、「変更しなかった」場合の的中率は約37％となり、結果に大幅に差が出たことがわかりました。

そこで、どうして「変更した」場合の方が的中率が上がったのかを話し合いました。
 

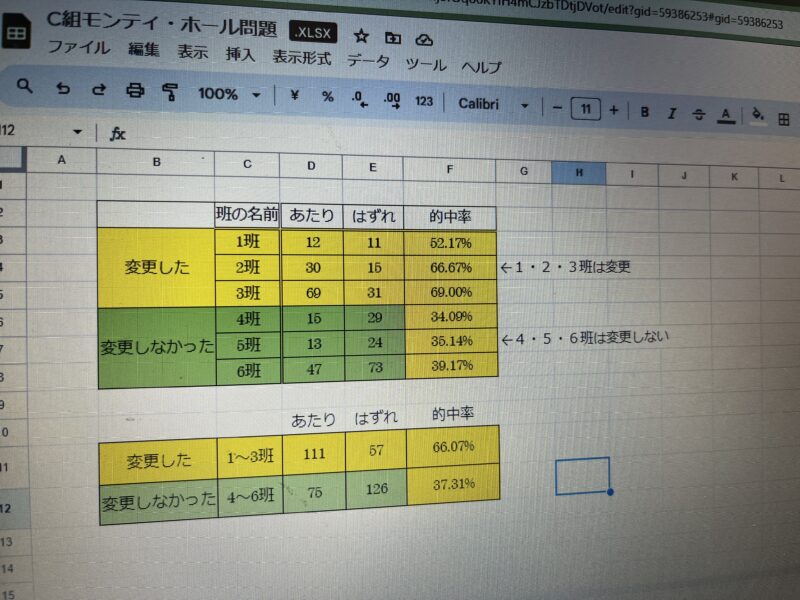
そうすると、「“最初から変更する”と決めれば、最初に2/3でハズレを引いてしまいさえすれば良い。逆に最初に1/3であたりを引いてしまうと外れてしまう。」などの、様々な意見が出ました。
楽しそうに実験してくれたのでよかったです。次の授業では、立式して確率を求めていきます。

（数学担当　教諭Ｏ）